【解説】
次の図のように，三角形の頂点を通らない1つの直線と，△ABCの辺AB，BC，CAまたはその延長との交点をそれぞれP，Q，Rとします。
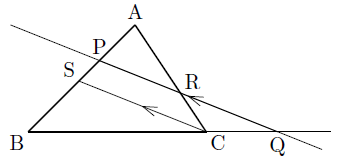
さらに，△ABCの頂点Cを通り，直線PQに平行な直線を引き，ABとの交点をSとすると，平行線と線分の比の関係から，
BQ:QC=BP:PS，CR:RA=SP:PA
となるので，
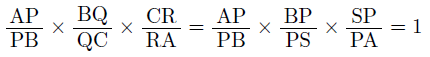
という関係が成り立ち，これをメネラウスの定理といいます。
【例題】
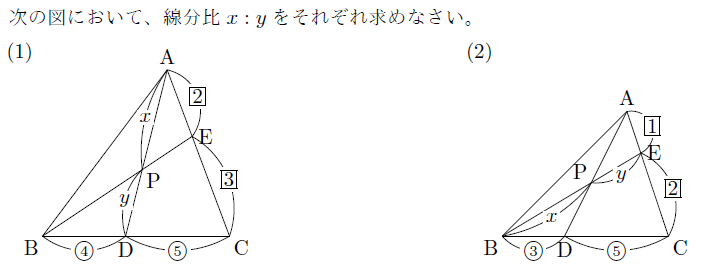
【無料動画講義（理論）】
【演習問題】
メネラウスの定理
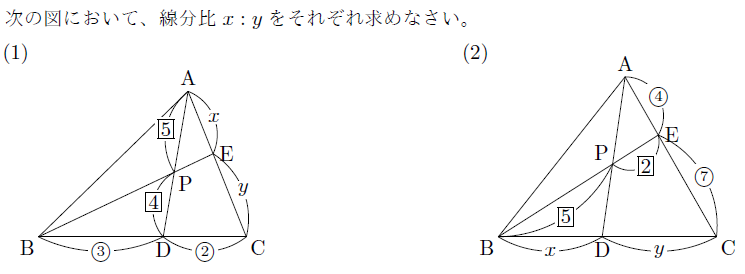
次の図のように，三角形の頂点を通らない1つの直線と，△ABCの辺AB，BC，CAまたはその延長との交点をそれぞれP，Q，Rとします。
さらに，△ABCの頂点Cを通り，直線PQに平行な直線を引き，ABとの交点をSとすると，平行線と線分の比の関係から，
BQ:QC=BP:PS，CR:RA=SP:PA
となるので，
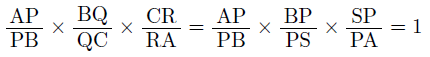
という関係が成り立ち，これをメネラウスの定理といいます。