【講義】直交条件
- 正解率:22.64%
- 解答数:106
EXAMPLE
例題
次の直線と垂直になる直線の傾きを求め,ア~オに当てはまる数を半角英数字で入力しなさい。ただし,
TEXT
テキスト解説
次の図のように,原点Oを通る傾き
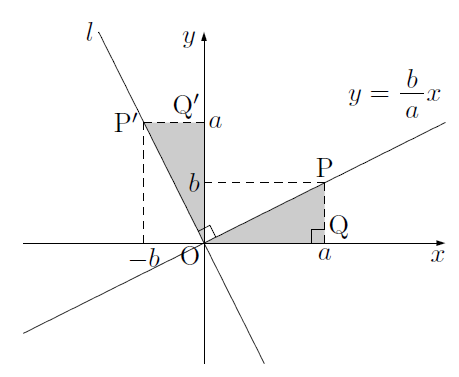
直線
このことから,直線
より,2直線の傾きを
という関係が成り立つことになります。
MOVIE
動画解説
次の直線と垂直になる直線の傾きを求め,ア~オに当てはまる数を半角英数字で入力しなさい。ただし,
次の図のように,原点Oを通る傾き

直線
このことから,直線
より,2直線の傾きを
という関係が成り立つことになります。