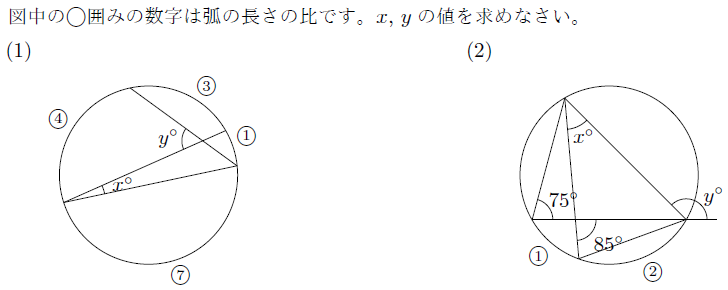
【解説】
次の図のおうぎ形OABとおうぎ形OCDのように,1つの円において,等しい長さの弧をもつ2つのおうぎ形は合同になるため,中心角の大きさは等しく,
![]() =
=![]() ならば∠AOB=∠COD
ならば∠AOB=∠COD
となります。
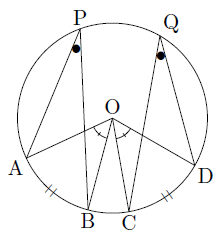
また,円周角の定理より,円周角は中心角の半分の大きさになるので,上の図のように,円周上に点P,Qがあるとき,
∠APB=1/2∠AOB,∠CQD=1/2∠COD
となります。∠AOB=∠CODであることから,
∠APB=∠CQD
という関係が成り立ち,同じ長さの弧であれば円周角の大きさも等しくなることがわかります。
このことから,この長さが2倍,3倍,…されると,その弧に対する中心角・円周角の大きさは2倍,3倍,…となり,弧の長さとその弧に対する中心角・円周角の大きさは比例します。
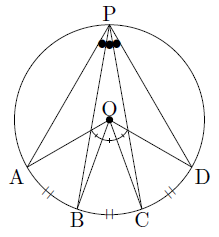
 =2
=2 :∠AOC=2∠AOB,∠APC=2∠APB
:∠AOC=2∠AOB,∠APC=2∠APB =3
=3 :∠AOD=3∠AOB,∠APD=3∠APB
:∠AOD=3∠AOB,∠APD=3∠APB
【例題】

【無料動画講義(理論)】
【演習問題】